AviralGarg.com

Introduction to Reinforcement Learning

Resources:

Recap

  1. How do you obtain your reward function in RLHF?
    • Collect human feedback through comparisons of model outputs
    • Human reviewers rank or compare outputs
    • Preferences are used to train a reward model
  2. What do you use the reward function for?
    • Fine-tune the LLM to generate preferred outputs
    • Adjust model parameters to maximize the reward
    • Encourage outputs that align with human preferences

Agenda Overview

  1. Introduction to Reinforcement Learning
    • Motivation and key concepts
    • Tools for experimenting with RL (e.g., Gymnasium)
    • Key ingredients: States, Actions, Rewards
    • Running Example: Blackjack
    • Introduction and rules of the game
    • Teaching an agent to play using RL
  2. Markov Decision Processes (MDPs)
    • Modeling sequential decision-making problems
    • Fundamental framework without learning algorithms
    • Applying MDPs to Blackjack
    • Deriving optimal strategies
    • Challenges of explicit modeling
  3. Q-Learning
    • Introduction to value-based RL methods
    • Understanding the Q-Learning algorithm
    • Applying Q-Learning to the Blackjack example
  4. Deep Q-Learning
    • Extending Q-Learning to handle larger state spaces
    • Conceptual differences from tabular Q-Learning
    • Applications in complex environments (e.g., video games)
    • Implementation details and code examples

Learning Objectives

Reinforcement Learning Introduction

Thought Exercise: Dice Game

The considerations to make when thinking about a strategy to play this game are similar to what gets modeled in Markov Decision Processes.

Applications of Reinforcement Learning

Key Concepts of Reinforcement Learning

Differences from Other Machine Learning Paradigms

Types of Reinforcement Learning Methods

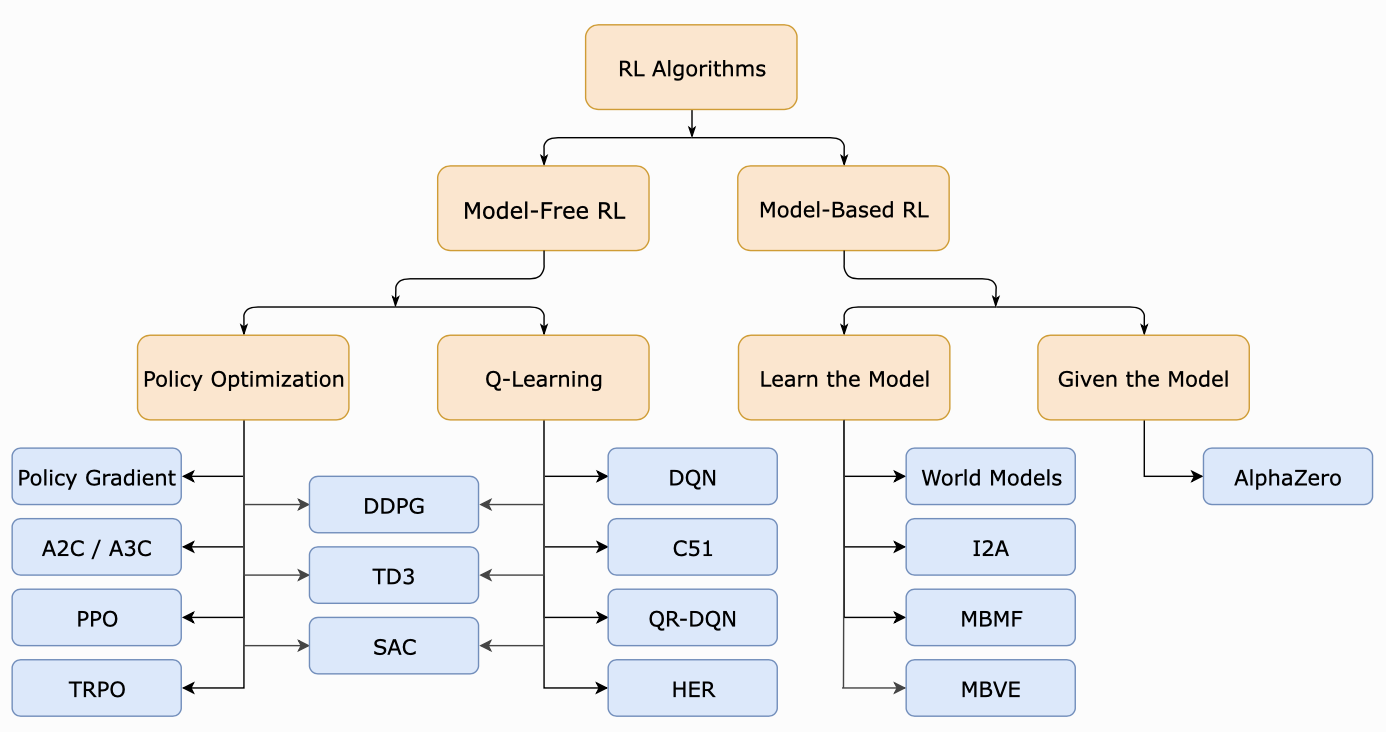
alt text

Tools for Reinforcement Learning: Gymnasium

import gymnasium as gym
env = gym.make("LunarLander-v2", render_mode="human")
observation, info = env.reset(seed=42)
for _ in range(1000):
    action = env.action_space.sample() # this is where you would insert your policy
    observation, reward, terminated, truncated, info = env.step(action)

    if terminated or truncated:
        observation, info = env.reset()

env.close()

Running Example: Blackjack Environment

Blackjack Rules Recap

Blackjack Environment Code

Gymnasium (formerly OpenAI Gym) is a popular toolkit for testing reinforcement learning algorithms. It provides simulation environments for a variety of RL tasks and a simple common interface for interacting the environments. In this notebook we will work with the Blackjack environment, which plays the popular casino game Blackjack. We will introduce the basic mechanics of the Gymnasium Blackjack environment by manually playing a hand.

# First we will install the Gymnasium package
# !pip install gymnasium

import gymnasium as gym
import torch
import torch.nn.functional as F

import random
import numpy as np
from IPython import display
from collections import deque, OrderedDict
import matplotlib.pyplot as plt

"""
Here we interact directly with the Blackjack environment to get
a feel for how it works
"""

# Create the environment
env = gym.make("Blackjack-v1", render_mode="rgb_array")

# Deal the cards / sample an initial state
obs = env.reset()[0]

# Render a visualization in the notebook
plt.imshow(env.render())
plt.show()
print(obs)

# Loop as long as the hand has not finished
done = False
while not done:

    # Choose an action: 1 is hit, 0 is stand
    action = int(input("Hit (1) / Stand (0): "))

    # Provide the action to the environment and update the game state
    # The environment returns three values that we care about:
    # - obs: The current state (or "observation", equivalent in this case)
    # - reward: The reward earned in the current step
    # - done: A boolean indicating whether the hand is done or in-progress
    obs, reward, done, truncated, info = env.step(action)

    # Render the updated state in the notebook
    display.clear_output(wait=True)
    plt.imshow(env.render())
    plt.show()
    print(obs, reward, done, truncated, info)

env.close()

A few notes to take away:

Interacting with the Blackjack Environment

Implementing a Simple Policy

The aim of Reinforcement Learning is to learn effective strategies for automatically selecting an action in each time period based on the current state of the environment. Rules for selecting an action based on the current state are known as policies. Here, we will manually create a simple heuristic policy and demonstrate how it controls the environment. We will evaluate this policy by playing 50,000 hands of Blackjack and counting the fraction of hands won under this policy.

def simple_policy(state):
    """
    This simple policy always hits (draws another card) if the total value of
    the player's hand is less than 17, and stays if the value of the player's
    hand is greater than or equal to 17.
    """

    # The first component of the state is the player's hand
    # If that is less than 17, hit. Otherwise stay.
    if state[0] < 17:
        return 1
    else:
        return 0

Running Simulations

Key Elements in Reinforcement Learning

States

Actions

Rewards

State Transitions

Generalizing to Multi-Stage Decision Problems

Markov Decision Processes (MDPs)

Definition

Time Horizons in MDPs

Episodic Tasks

Continuing Tasks

Modeling Episodic Tasks as Continuing Tasks

Simplifying the Reward Structure

Discounted Rewards

Expected Total Discounted Reward

Importance of Discount Factor ($ \gamma $)

Solving MDPs

Policies

Value Functions

The Bellman Equation

Summary